posteriormean()

subroutine, public ompi_kronlininv::posteriormean	(	real(dp), dimension(:,:), intent(in)	U1,
		real(dp), dimension(:,:), intent(in)	U2,
		real(dp), dimension(:,:), intent(in)	U3,
		real(dp), dimension(:), intent(in)	diaginvlambda,
		real(dp), dimension(:,:), intent(in)	Z1,
		real(dp), dimension(:,:), intent(in)	Z2,
		real(dp), dimension(:,:), intent(in)	Z3,
		real(dp), dimension(:,:), intent(in)	G1,
		real(dp), dimension(:,:), intent(in)	G2,
		real(dp), dimension(:,:), intent(in)	G3,
		real(dp), dimension(:), intent(in)	mprior,
		real(dp), dimension(:), intent(in)	dobs,
		real(dp), dimension(:), intent(out)	postm
	)

Computes the posterior mean

Parameters

[in]	U1,U2,U3	\( \mathbf{U}_1 \), \( \mathbf{U}_2 \), \( \mathbf{U}_3 \) of \( F_{\sf{A}} \)
[in]	diaginvlambda	\( F_{\sf{B}} \)
[in]	Z1,Z2,Z3	\( \mathbf{U}_1^{-1} \mathbf{C}_{\rm{M}}^{\rm{x}} (\mathbf{G}^{\rm{x}})^{\sf{T}}(\mathbf{C}_{\rm{D}}^{\rm{x}})^{-1} \), \( \mathbf{U}_2^{-1} \mathbf{C}_{\rm{M}}^{\rm{y}} (\mathbf{G}^{\rm{y}})^{\sf{T}} (\mathbf{C}_{\rm{D}}^{\rm{y}})^{-1}\), \( \mathbf{U}_3^{-1} \mathbf{C}_{\rm{M}}^{\rm{z}} (\mathbf{G}^{\rm{z}})^{\sf{T}} (\mathbf{C}_{\rm{D}}^{\rm{z}})^{-1} \) of \( F_{\sf{D}} \)
[in]	G1,G2,G3	The 3 forward modeling matrices \( \mathbf{G} = \mathbf{G_1} \otimes \mathbf{G_2} \otimes \mathbf{G_3} \)
[in]	mprior	Prior model (vector)
[in]	dobs	Observed data (vector)
[out]	postm	Calculated posterior mean model (vector)

Date

5/8/2016 - Initial Version

27/12/2016 - New ETA calculations

18/1/2017 - OpenMPI version

Definition at line 949 of file ompi_kronlininv.f08.

    !!
    use parautil
    
    !!
    !! Calculate the posterior mean model
    !! 
    real(dp),intent(in)  :: u1(:,:),u2(:,:),u3(:,:), g1(:,:),g2(:,:),g3(:,:)
    real(dp),intent(in)  :: z1(:,:),z2(:,:),z3(:,:)
    real(dp),intent(in)  :: mprior(:),dobs(:),diaginvlambda(:)
    real(dp),intent(out) :: postm(:)

    real(dp),allocatable :: ddiff(:),ddiffmpi(:),postmmpi(:)
    integer :: a,b,na,nb
    integer :: ni,nj,nk,nl,nm,nn

    integer,allocatable :: av(:),bv(:)
    integer,allocatable :: iv(:),jv(:),kv(:),lv(:),mv(:),nv(:)
        !! ivo(:),jvo(:),kvo(:)
    integer :: p,everynit

    real(dp),allocatable :: zh(:),eludzh(:),zhmpi(:),eludzhmpi(:)

    integer :: ia,ib
    real(dp) :: startt,firststartt,endt
    character(len=30) :: loopinfo
    
    integer ::curit,totit
    integer,allocatable :: scheduling(:),looping(:,:)

    !! sizes
    ni = size(z1,1)
    nl = size(z1,2)
    nj = size(z2,1)
    nm = size(z2,2)
    nk = size(z3,1)
    nn = size(z3,2)

    !! sizes
    ! Nr12 = size(U1,2)*size(U2,2)*size(U3,2)
    ! Nc1  = size(Z1,1)*size(Z2,1)*size(Z3,1)
    na = size(mprior,1) 
    nb = size(dobs,1)
    
    !! allocate stuff
    allocate(ddiff(nb))
    allocate(zh(na),eludzh(na))
 
    !! vectorize row and col calculations for Kron prod AxBxC
    !!allocate(ivo(Nb),jvo(Nb),kvo(Nb))
    allocate(av(na),iv(na),jv(na),kv(na))
    allocate(bv(nb),lv(nb),mv(nb),nv(nb))
    forall(p = 1:na) av(p) = p
    forall(p = 1:nb) bv(p) = p

    !! vectors containing all possible indices for 
    !!    row calculations of Kron prod AxBxC
    iv =  (av-1)/(nk*nj)+1 
    jv =  (av-1-(iv-1)*nk*nj)/nk+1 
    kv =  av-(jv-1)*nk-(iv-1)*nk*nj 
    !! vectors containing all possible indices for
    !!    column calculations of Kron prod AxBxC
    lv =  (bv-1)/(nn*nm) + 1 
    mv =  (bv-1-(lv-1)*nn*nm)/nn + 1 
    nv =  bv-(mv-1)*nn-(lv-1)*nn*nm 
    !!  Gs have different shape than Us !!

    !!#######################
    if (na<1000)then
       everynit = na/50
    else if (na<100000) then
       everynit = na/100
    else
       everynit = na/1000
    end if

    !!---------------------------------
    firststartt = mpi_wtime()

    !!#######################
    !!#    dobs - dcalc     #
    !!#######################
    startt = mpi_wtime()    
    loopinfo = "posteriormean(): loop 1/3"
    if (myrank==masterrank) write(output_unit,*)
    !! calculate scheduling for Nb
    call spreadwork(nb,numcpus,scheduling,looping,1)
    allocate(ddiffmpi(scheduling(myrank+1)))
    !! difference obs-calc data
    totit = looping(myrank+1,2)-looping(myrank+1,1)
    do b=looping(myrank+1,1),looping(myrank+1,2) !! rank starts from 0
       curit = (b-looping(myrank+1,1)+1)
       if ( (myrank==masterrank) .and. (mod( curit,everynit)==0) ) then          
          call timeinfo(totit,curit,startt,loopinfo)
       end if
       
       !!--------------------------------------------------------------------------------
       ib = b - looping(myrank+1,1) + 1 
       ddiffmpi(ib) = dobs(b) - sum(mprior * g1(lv(b),iv) * g2(mv(b),jv) * g3(nv(b),kv))
       !!--------------------------------------------------------------------------------

    end do

    startt = mpi_wtime()    
    !! assemble full ddfiff and broadcast it
    !! displacements  must start from 0, not 1, so looping-1
    call para_allgathv1ddp( scheduling,looping(:,1)-1, ddiffmpi, ddiff )
    if (myrank==masterrank) then
       print*,"time for first allgatherv:",mpi_wtime()-startt,"s"
    end if

    
    !!#######################
    !!#   === U d Z h ===   #
    !!#######################
    startt = mpi_wtime()    
    !! calculate scheduling for Na
    loopinfo = "posteriormean(): loop 2/3"
    if (myrank==masterrank) write(output_unit,*)
    call spreadwork(na,numcpus,scheduling,looping,1)
    allocate(zhmpi(scheduling(myrank+1)))
    totit = looping(myrank+1,2)-looping(myrank+1,1)
    do a=looping(myrank+1,1),looping(myrank+1,2) !! rank starts from 0
       curit =(a-looping(myrank+1,1)+1)
       if ( ( myrank==masterrank ) .and. (mod( curit,everynit)==0) ) then       
          call timeinfo(totit,curit,startt,loopinfo)
       end if

       !!---------------------------------------------------------------------------
       ia = a - looping(myrank+1,1) + 1
       zhmpi(ia) = sum( z1(iv(a),lv) * z2(jv(a),mv) * z3(kv(a),nv) * ddiff )
       !!---------------------------------------------------------------------------
       
    end do

    startt = mpi_wtime()
    !! assemble full Zh and broadcast it
    call para_allgathv1ddp( scheduling,looping(:,1)-1, zhmpi, zh )
    if (myrank==masterrank) then
       print*,"time for second allgatherv:",mpi_wtime()-startt,"s"
    end if
    
    !!-----------------------------------------------
    !! Second loop
    !!### need to re-loop because full Zh is needed
    !!#######################
    !!#       post(a)       #
    !!#######################
    startt = mpi_wtime()
    !! calculate scheduling for Na
    loopinfo = "posteriormean(): loop 3/3"
    if (myrank==masterrank) write(output_unit,*)
    call spreadwork(na,numcpus,scheduling,looping,1)
    allocate(eludzhmpi(scheduling(myrank+1)),postmmpi(scheduling(myrank+1)))
    totit = looping(myrank+1,2)-looping(myrank+1,1)
    do a=looping(myrank+1,1),looping(myrank+1,2) !! rank starts from 0
       curit = (a-looping(myrank+1,1)+1)
       if ( ( myrank==masterrank ) .and. (mod(curit,everynit)==0) ) then
          call timeinfo(totit,curit,startt,loopinfo)
       end if

       !!--------------------------------------------------------------------------------------
       ia = a - looping(myrank+1,1) + 1
       !! 
       eludzhmpi(ia) = sum( u1(iv(a),iv) * u2(jv(a),jv) * u3(kv(a),kv) * diaginvlambda * zh )
       !! element of the posterior mean
       postmmpi(ia) = mprior(a) + eludzhmpi(ia)
       !!--------------------------------------------------------------------------------------
       
    end do

    startt = mpi_wtime()    
    !! assemble full postm only for masterrank
    call para_gathv1ddp( scheduling,looping(:,1)-1, masterrank, postmmpi, postm )
    if (myrank==masterrank) then
       print*,"time for third allgatherv:",mpi_wtime()-startt,"s"
    end if


    if (myrank==masterrank) then
       write(output_unit,*)
       write(output_unit,*)
       endt = MPI_Wtime()
       print*,"posteriormean():",endt-firststartt," MPI wall clock time"
    end if

    !print*,myrank,":",shape(ddiffmpi),shape(Zhmpi),shape(elUDZhmpi),shape(postmmpi),&
     !    shape(ddiff),shape(Zh),shape(elUDZh),shape(postm)

    return

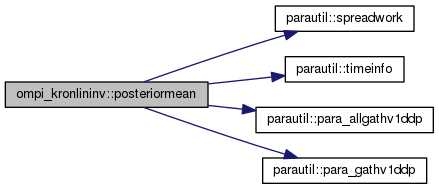
Here is the call graph for this function:

Here is the caller graph for this function: